- Published on
動的計画法(Dynamic Programming)をサルでも分かるように説明する - その1(フィボナッチ数列)
- Authors
- ジャバ・ザ・ハットリ

「動的計画法(Dynamic Programming、以下 DP)をどんな人にも分かるように丁寧に解説する」というこれまで何人もの優秀な方々が挑戦した内容にあえてまた参戦することにした。
「動的計画法」とか「Dynamic Programming」でググると山のように解説ページがヒットする。お決まりのセリフは「とてもカンタン」「誰にでも分かる!」しかし実情は難しいし、どの解説を読んでも「カンタンじゃねーよ」と思ってしまう。その理由について以下の仮説をたてた。
- 解説を書いている人は DP をカンタンに理解できるほど頭がいい
- 頭が良すぎて「読んでも分からない人の気持ち」が分からない
- 解説を読んで「オレならもっとカンタンに説明できるゼ!」という人が現れる
- そんな人もやっぱり頭がいいので1に戻る
- 以下、無限ループの繰り返しで、世の中に DP の解説が溢れる
これは DP の解説があり過ぎるからもう要らないのではなく、むしろどんどんよりカンタンで分かりやすい説明が必要とされていることの裏返しなのだと勝手に理解した。ということで書いた。
DP はアルゴリズムの最高峰??
もし DP を今まで聞いたことがない人のために分かりやすく説明すると「わりと難しいけど、使い所さえ掴めば便利な方法」と言える。こちらのウェブサイトに「Programmer Competency Matrix(プログラマ能力指標)」なるものが勝手に定義されている。
その定義によるとアルゴリズムに関しては
レベル0
配列に含まれる数値の平均値を求めることができない (信じ難いことですが、そんなプログラマ候補者と面接したことがあります)
レベル1
ソート、検索、データ構造トラバーサル、データ取り出しアルゴリズムの知識がある。
とかあって、最高レベルのがこれ。
最高レベル
DP ソリューションに気付いてコーディングすることができ、
グラフアルゴリズムや数値計算アルゴリズムの知識が豊富で、NP 問題などを特定できる。
まー真意の程はさておき、DP がよく分かっていて使いこなせると高レベルと認識されますよ、と。
フィボナッチ数列
最もカンタンな DP の実装例はフィボナッチ数列になる。これはどの解説でも同じ。最初の例はいつもフィボナッチ数列。
フィボナッチ数列とは
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,
前の2つの和が次の数字になる数列。自然界の現象にも存在する数列で小学生向けの中学入試なんかにも度々登場する。
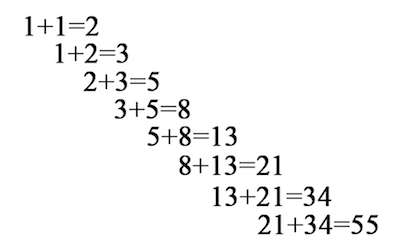
n 番目のフィボナッチ数列の数を求めるコードを書く。
なにも考えずに総当りの再帰で書くとこうなる。ここではこれを全探索版とする。
【全探索版】
def fib(n)
if n <= 1
return 1
else
fib(n-1) + fib(n-2)
end
end
ためしに puts で順番に出すと数列が出る。
puts fib(1)
puts fib(2)
puts fib(3)
puts fib(4)
puts fib(5)
puts fib(6)
puts fib(7)
puts fib(8)
puts fib(9)
結果
$ ruby fib.rb
1
2
3
5
8
13
21
34
55
しかしこの方法では計算量が多すぎて、まともに結果が返ってくるのはせいぜい40番目ぐらいまで。
このコードでは例えば7番目の数を出す際にはその手前の6番目と5番目の数を指す必要がある。6番目の数を出すには5番目と4番目が必要。5番目を出すには4番目を3番目が必要。と順番に全ての必要な数を繰り返し計算している。つまり 2n回分の計算が必要になる。
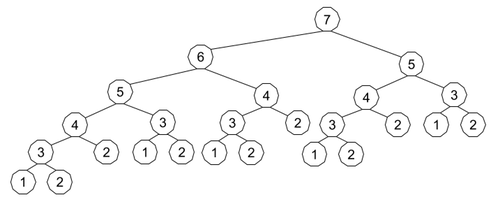
上の図で分かるように重複した数字を何度も計算している。
これを効率よく計算するのが DP。DP は大きく分けて2種類ある。
2種類の DP
- トップダウン:メモ化再帰、メモ化
- ボトムアップ:分割統治法、漸化式ループ
この2つに分けられる、とする。ここで「いやいや厳密に言うと**という方法があってだな」とやられるからややこしくなる。ここで2つに大別した方が後の理解がより容易くなる。
トップダウン:メモ化再帰
これは計算した結果を記録しておいて、同じ数に関しては1度しか計算しないようにする方法。
@f = []
def fib2(n)
if n <= 1
return 1
else
if @f[n]
return @f[n]
else
@f[n] = fib2(n-1) + fib2(n-2)
end
end
end
メモ(記録)して、それがあればそのまま出す。メモが無ければ計算してメモに入れておく、をしているのがこの箇所。
if @f[n]
return @f[n]
else
@f[n] = fib2(n-1) + fib2(n-2)
end
ただそれだけなのだが、ベンチマークで測るとすごい差が出る。
require 'benchmark'
Benchmark.bm(10) do |b|
b.report "fib" do
fib(35)
end
b.report "fib2 (DP)" do
fib2(35)
end
end
user system total real
fib 1.300000 0.000000 1.300000 ( 1.306700)
fib2 (DP) 0.000000 0.000000 0.000000 ( 0.000012)
これは当然のことで n=35 とかになっても DP 版は 35 回しか計算しない。それに引き換え、全探索版では 29,860,703 回の計算を行っている。
ボトムアップ:分割統治法、漸化式ループ
これは最初の再帰の処理において繰り返しがたくさん発生するのはトップダウンで上から下に向かって、計算することが原因としてある。逆に下から上に計算すれば1方向で何度も計算しなくて済む、という方法。
以下の図で言えば7から始めるから計算が多い。左下の1から上に上がっていけば少ない計算数で7まで辿り着く。

コードで書くとこのようになる。
def fib3(n)
if n==0
return 1
else
fib1 = fib2 = fib3 = 1
(n-1).times do
fib3 = fib1 + fib2
fib1 = fib2
fib2 = fib3
end
return fib2
end
end
やってることは単純で数列の一番の最初の1,1,から始めてそれらを足して次々に数を求め、n に達したら止める、と。
ベンチマークはこの通り。全探索版との差は一目瞭然。
user system total real
fib 1.900000 0.010000 1.910000 ( 1.904163)
fib3 (DP) 0.000000 0.000000 0.000000 ( 0.000009)
実は他にももっと計算量を少なくする書き方があるが、そこを議論しても DP の概念理解の助けにはあまりならない。まずは大きく分けて2つあるトップダウンとボトムアップの DP を理解することで次にすすめることができる。DP を理解するにはここの例で示したのとまったく同じ手順を繰り返すこと。すなわち
- 問題を全探索で解く(実際にコードを書かなくても頭の中で考える)
- 全探索版を「トップダウン:メモ化再帰」にする
- もしくは全探索版を「ボトムアップ:漸化式ループ」にする
少なくとも私は上記のフローにしたがって学習することで少しずつ理解できた。
だいたいはここまではカンタンに理解できる。難しいのはこれらの知識を他の問題に応用したりするところ。それは次回以降ということで。